Bluegrass Volunteer Examiners                        
     N8UK & KN4S

This page was last updated 12/09/2014 06:26 PM
You are visitor number

Home
Amateur Exams
Commercial Exams
BVE Group
Links
Repeater Info
RF Safety
RADIATION PROBE
Skywarn Info
Title IV-Spam
UK Wildcat Page
About KN4S
Session Info

RF Safety Certification Information

Additional Information for Amateurs Completing the New FCC Form 605
Reprinted from ARRL VEC VE Express, Winter 1997/98 - No. 2

The new FCC Form 605 requires that all applicants now sign an RF Safety Certification. The certification that applicants must now sign reads: "I have READ and WILL COMPLY with Section 97.13(c) of the Commission's Rules regarding RADIO FREQUENCY (RF) RADIATION SAFETY and the amateur service section of OST/OET Bulletin Number 65." This is all well and good, but how can you sign this statement if you haven't seen these new rules and Bulletin 65 information? Unfortunately, the FCC has not provided this additional information in the instructions to the new Form 605.

Recognizing this need, here is the information you will need to read and must comply with. Section 97.13(c) reads:

  c. Before causing or allowing an amateur station to transmit from any place where the operation of the station could cause human exposure to RF electromagnetic field levels in excess of those allowed under §1.1310 of this chapter, the licensee is required to take certain actions.

     1. The licensee must perform the routine RF environmental evaluation prescribed by §1.1307(b) of this chapter, if the power of the licensee's station exceeds the limits given in the following table:

--Repeater stations (all bands) non-building mounted antennas: height above ground level to
lowest point of antenna < 10m and power > 500W ERP

--Building-mounted antennas: power > 500W ERP

*Power = PEP input to antenna except, for repeater stations only, power exclusion is based on ERP (effective radiated power).

     2. If the routine environmental evaluation indicates that the RF electromagnetic fields could exceed the limits contained in §1.1310 of this chapter in accessible areas, the licensee must take action to prevent human exposure to such RF electromagnetic fields.  Further information on evaluating compliance with these limits can be found in the FCC's OET Bulletin 65, "Evaluating Compliance with FCC-Specified Guidelines for Human Exposure to Radio Frequency Electromagnetic Fields."

The Amateur Section of OET Bulletin Number 65:

In the FCC's Report and Order, certain amateur radio installations were made subject to routine evaluation for compliance with the FCC's RF exposure guidelines.¹   Also, amateur licensees will be expected to demonstrate their knowledge of the FCC guidelines through examinations.  Applicants for new licenses and renewals also will be required to demonstrate that they have read and that they understand the applicable rules regarding RF exposure.  Before causing or allowing an amateur station to transmit from any place where the operation of the station could cause human exposure to RF radiation levels in excess of the FCC guidelines, amateur licensees are now required to take certain actions.  A routine RF radiation evaluation is required if the transmitter power of the station exceeds the levels shown and specified in 47 CFR §97.13(c)(1)²(see above).  Otherwise the operation is categorically excluded from routine RF radiation evaluation, except as a result of a specific motion or petition as specified in Sections 1.1307(c) and (d) of the FCC's Rules, (see discussion in Section 1 of Bulletin 65 for more information).

The Commission's Report and Order instituted a requirement that operator license examination question pools will include questions concerning RF safety at amateur stations.  An additional five questions on RF safety will be required within each of three written examination elements (for Novice, Technician and General written exams).

When routine evaluation of an amateur station indicates that exposure to RF fields could be in excess of the exposure limits specified by the FCC (see Bulletin 65, Appendix A), the licensee must take action to correct the problem and ensure compliance (see Section 4 of Bulletin 65 on controlling exposure).  Such actions could be in the form of modifying patterns of operation, relocating antennas, revising a station's technical parameters such as frequency, power or emission type or combinations of these and other remedies.

Bulletin 65, Appendix A, Table 1 -- LIMITS FOR MAXIMUM PERMISSIBLE EXPOSURE (MPE)

Limits for Occupational/Controlled Exposure
(f=frequency in MHz   :   *Plane-wave equivalent power density)

Limits for General Population/Uncontrolled Exposure
(f=frequency in MHz  :  *Plane-wave equivalent power density)

In complying with the Commission's Report and Order, amateur operators should follow a policy of systematic avoidance of excessive RF exposure.  The Commission has said that it will continue to rely upon amateur operators, in constructing and operating their stations, to take steps to ensure that their stations comply with the MPE limits for both occupational/controlled and general public/uncontrolled situations, as appropriate.   In that regard, amateur radio operators and members of their immediate household are considered to be in a "controlled environment" and are subject to the occupational/controlled MPE limits.  Neighbors who are not members of an amateur operator's household are considered to be members of the general public, since they cannot reasonably be expected to exercise control over their exposure.  In those cases general population/uncontrolled exposure MPE limits will apply.

In order to qualify for use of the occupational/controlled exposure criteria, appropriate restrictions on access to high RF field areas must be maintained and educational instruction in RF safety must be provided to individuals who are members of the amateur operator's household.  Persons who are not members of the amateur operator's household but who are present temporarily on an amateur operator's property may also be considered to fall under the occupational/controlled designation provided that appropriate information is provided them about RF exposure potential if transmitters are in operation and such persons are exposed in excess of the general population/uncontrolled limits.

Amateur radio facilities represent a special case for determining exposure, since there are many possible antenna types that could be designed and used for amateur stations.   However, several relevant points can be made with respect to analyzing amateur radio antennas for potential exposure that should be helpful to amateur operators in performing evaluations.

First of all, the generic equations described in Bulletin 65 can he used for analyzing fields due to almost all antennas, although the resulting estimates for power density may be overly-conservative in some cases.  Nonetheless, for general radiators and for aperture antennas, if the user is knowledgeable about antenna gain, frequency, power and other relevant factors, the equations in this section can he used to estimate field strength and power density as
described earlier.  In addition, other resources are available to amateur radio operators for analyzing fields near their antennas.  The ARRL Handbook For Radio Amateurs contains an excellent section on analyzing amateur radio facilities for compliance with RF guidelines.  Also, the FCC and the EPA conducted a study of several amateur radio stations in 1990 that provides a great deal of measurement data for many types of antennas commonly used by amateur operators³ (see the FCC OET Web site at:  http://www.fcc.gov/oet/info/documents/reports/#ASD-9601 see also http://www.fcc.gov/oet/rfsafety/).

Amateur radio organizations and licensees are encouraged to develop their own more detailed evaluation models and methods for typical antenna  configurations and power/frequency combinations.  The FCC has an Amateur Supplement "B" that is available from the FCC's OET Web site at http://www.fcc.gov/oet/rfsafety/.   Information on availability of the supplement, as well as other RF-related questions, can be directed to the FCC's "RF Safety Program" at: (202) 418-2464 or Email to: rfsafety@fcc.gov.

See also: Sections 1 and 2 of the FCC Regulations; FCC's "Amateur" Supplement B to OET Bulletin 65; the ARRL's publication entitled "RF Exposure and You" (to be available in early 1998); the ARRLWeb at:  http://www.arrl.org/news/rfsafety/; and our RF Safety article in January 1998 QST (Pages 50-55) for more information.

[footnotes]-

¹ See para. 160 of Report and Order, ET Dkt 93-62. See also, 47 CFR § 97.13, as amended.

² These levels were chosen to roughly parallel the frequency of the MPE limits of Table 1 in Appendix A. These levels were modified from the  Commission's original decision establishing a flat 50 W power threshold for routine evaluation of amateur stations (see Second Memorandum Opinion and Order, ET Docket 93-62, FCC 97-303, adopted August 25, 1997).

³ Federal Communications Commission (FCC), "Measurements of Environmental Electromagnetic Fields at Amateur Radio Stations," FCC Report No. FCC/OET ASD-960l, February 1996. FCC, Office of Engineering and Technology (OET), Washington, D.C. 20554. NTIS Order No. PB96-145016. Copies can also be downloaded from OET's Home Page on the World Wide Web at:  http://www.fcc.gov/oet/.

Near-Field Electromagnetic Radiation Probes for Amateur Radio

by David S. Forsman, WA7JHZ, and Michael D. Tarola, KB7CP

Build these simple 1.8 to 29.7 MHz electromagnetic probes to determine your FCC OET-65B near-field radiation compliance using a common 10 M ohm digital voltmeter (DVM). The DVM and probes are connected through special cables composed of twenty (each) 100 K ohm resistors spaced at 10 cm intervals, insulated with plastic tubing, and placed inside one-meter (1m) lengths of 1/2 inch PVC water pipe (see drawing below). These cables resistively isolate the probes from the DVM at radio frequencies, while also reducing their own parasitic antenna tendencies.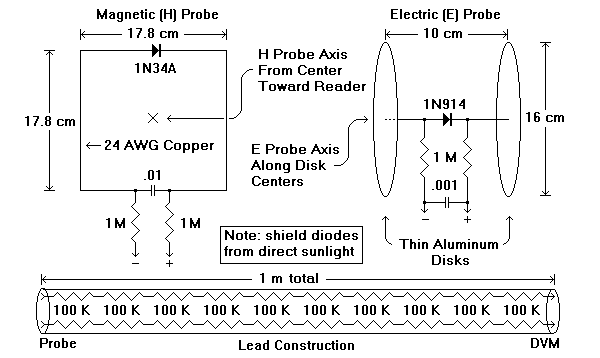



Pay careful attention to the use of the 1N34A germanium diode for the magnetic (H) probe and the 1N914 silicon switching diode for the electric (E) probe. The 1N34A diode gives excellent low-voltage sensitivity to the H probe while allowing it to measure in excess of 1.63 A/m, and the 1N914 provides low junction capacitance and high-voltage capability to the E probe, thus allowing it to measure a maximum (peak) level of 350 V/m. Avoid using substitute diode types, since they can severely alter the overall performance.

These probes measure both the magnetic (H) and electric (E) components of your antenna's near-field radiation in units of amps-per-meter (A/m) magnetic, or volts-per-meter (V/m) electric. The following formulas are used to convert your DVM's voltage reading (or Vdc) to initial H and E values: H (A/m) = 4(Vdc + 0.05)/f (f in MHz), and E (V/m) = 10(Vdc + 0.3). For example, if your magnetic (H) probe produced a Vdc reading of 1.5 volts on your DVM at 3.8 MHz, then your initial H field value would be 1.63 A/m (4 x (1.5 V + 0.05)/3.8mhz = 1.63 A/m). For the E probe, you would use the second formula--the E probe, within the amateur bands from 1.8 to 29.7 MHz, is not frequency dependent. We will cover the formula derivations in later paragraphs.

Like a dipole antenna, these probes are polarized, in that they produce maximum Vdc readings when their axes are in the same polarity as that of the near-field. But most practical antennas exhibit a complex near-field. Because of this, a probe's Vdc value might have more than one maximum as its axis is aligned within a given field (the H probe's axis is an imaginary line passing directly through, and at right angles to, the imaginary plane of its open center, while the E probe's axis is an imaginary line passing directly through the centers of its two aluminum disks).

For "quick-method" measurements, while transmitting a continuous-wave (CW) signal (not Morse code), orient a probe at the measurement point to maximize Vdc on your DVM. This will require experimentally rotating the probe's axis through several different vertical and horizontal angles until you find Vdc max. Then, after calculating the conversion value from Vdc (and possibly f), multiply it by 1.732--the square root of 3. For single-element vertical antennas, it is easy to find the Vdc maximum--but the quick-method often overestimates simple near-field values.

For a second approach, imagine a three-dimensional Cartesian coordinate set (x, y, z) with its origin centered at the measurement point (see drawing below); position and read a probe with its axis aligned once with each of the imaginary x, y, and z axes at the measurement point; calculate the initial conversion values (three total); and apply them to the root-sum-squared (RSS) formula, sqrt(a^2 + b^2 + c^2). This process adds the three vector magnitudes of the mutually orthogonal initial probe values. The result should fall between 57% and 100% of the quick-method value. This procedure, unlike the quick-method, should minimize the errors associated with complex fields, but it does requires more work.



Since these probes are best at indicating the average value of the H or E level, it is necessary to make measurements with a CW (steady carrier) signal, and then apply "peak value" multipliers to the value(s) based on the desired modulation method--AM, FM, SSB, etc. For instance, if you arrive at a final E value of 100 V/m from a CW signal that represents the zero-modulation carrier level of an AM signal, you would multiply the 100 V/m E value by two (x 2). This would represent the AM peak E value at 100% modulation (2 x 100 V/m = 200 V/m @ 100% modulation). However, if the same CW level represents the peak value of an equivalent SSB signal, then no multiplier is necessary--the peak SSB E level would also be 100 V/m.

On the lower-frequency amateur bands (160-75 m), where higher E values are allowed, the 350 V/m limit of the E probe can be compensated for by doing the following: lower the CW power output of the test transmitter until the E value is either equal to, or less than, 350 V/m; square the value of the ratio of the maximum allowable E field and the actual E field; and multiply this quantity by the new power level to determine the maximum power level at the maximum allowable E level (((Emax/Eactual)^2) x Watts = Watts max).

For example, suppose we have to reduce our transmitter output to 100 Watts to get 300 V/m at 1.9 MHz (160 m). Since we are allowed a controlled level of 614 V/m on this band, we square the ratio of 614 V/m and 300 V/m, and multiply this by 100 Watts to get 418 Watts (((614/300)^2) x 100 = 418 Watts). As long as we don't exceed 418 Watts peak output on 1.9 MHz, our E value won't exceed 614 V/m. Remember, also, that the uncontrolled E level at 1.9 MHz is only 433 V/m. This would represent a maximum peak power level of 208 Watts (((433/300)^2) x 100 = 208 Watts). Regardless of calculation, 1500 Watts is the maximum allowable peak power level, and some bands are even less. But, you may still be asking, "What makes them work?"

The H probe's characteristics are defined by Vo =wBs (from Faraday's Law), where Vo is induced loop voltage; w = 2(pi)f (f in Hz); B is magnetic field strength in Webers-per-square-meter (W/m^2); and s is loop area in square meters (Marshall 294). Since we prefer H, or magnetic field intensity in A/m units instead of B, we will use the definition B =uH, where u = 4(pi)x 10^-7 henry/m (Units 3-12, 3-14). This then gives us Vo =wuHs = 2(pi)f(4(pi)x 10^-7 henry/m)Hs. We can approximate this relationship as Vo = 7.896fHs, with f in MHz.

Solving for H, we get H = Vo/(7.896fs). For our 17.8 cm square probe, we get H = 4Vo/f. The resulting rectified DC voltage from the 1N34A is approximately 1.4 times the induced RMS Vo voltage, but the 4 M ohms of probe and lead resistance combined with the 10 M ohm DVM resistance give a voltage division of 1.4, so that Vdc could represent Vo, or Vdc = 1.4Vo/1.4. By substituting Vdc for Vo, we get H = 4Vdc/f. To compensate for low-signal 1N34A diode cutoff voltage error, we add 0.05 V to the Vdc value. This finally gives us H = 4(Vdc + 0.05)/f. Note, also, the importance of the H probe's 0.01 uF capacitor that attenuates unwanted E field response.

The E probe's characteristics are defined by Vdif = Ed, where Vdif is the voltage differential between plates and d is plate spacing in meters (m). In an E field, this probe is a capacitive voltage divider, where the capacitance of its plates (1.8 pF) is designed greater than the junction capacitance of the 1N914 diode (less than 1 pF). In an E field, where electric field intensity is given in volt-per-meter (V/m) units, you would find a voltage differential, Vdif, equal to the value of E between any two points spaced one-meter (1m) apart within the length of the field. Our probe is spaced at 10 cm (d = 0.1 m), so it intercepts one-tenth of the differential (Vdif = E x 0.1 m).

Solving for E, we get E = Vdif/d. For our 10 cm spacing (d = 0.1 m), E = Vdif/0.1 = 10Vdif. The resulting rectified DC voltage is approximately 1.4 times the RMS Vdif voltage, but, again, the 4 M ohms of probe and lead resistance combined with the 10 M ohm DVM resistance give us a voltage division of 1.4 so that Vdc can also represent Vdif, or Vdc = 1.4Vdif/1.4. By substituting Vdc for Vdif, we get E = 10Vdc. To adjust for the 1N914 cutoff voltage error, we add 0.3 V to the Vdc value, or E = 10(Vdc + 0.3).

The diode cutoff voltage error values for the 1N34A and 1N914 were made with empirical AC to DC voltage conversion measurements at 60 Hz. Using both a low-distortion audio oscillator and an adjustable autotransformer line voltage source, both diodes were individually fed with differing levels of 60 Hz voltage; their corresponding DC output voltages were then filtered by a 1 uF capacitor with the output coupled to a 10 M ohm Fluke model 75 DVM through a 4 M ohm resistor. This circuit models the dynamic conditions that the diodes would normally be subjected to in the probes, but at 60 Hz. Finally, the AC and DC voltage readings were compared to determine their voltage differences. The 0.05 V of the 1N34A and the 0.3 V of the 1N914 represent "worse case" error values that affect the accuracy--especially when measuring at low field intensity levels.

By giving our H probe only one turn, and using a 0.01 uF capacitor across its output, we avoid the need to electrically shield it from E fields. Though it does lack the sensitivity of multi-turn H probes, it is difficult to predict the characteristics of shielded multiple-turn H probes at higher frequencies because of the effects of distributed capacitance. By keeping it simple, our H probe (within limits) should better maintain the characteristics of its basic definition.

For the E probe, its simple fundamental design helps to overcome the detector diode's internal junction capacitance. An ideal E probe detector diode (or any diode) would have zero junction capacitance and cutoff voltage, plus infinite reverse voltage breakdown--but not yet possible. Some types of Schottky diodes have lower junction capacitances than the 1N914, but many have lower breakdown voltages. It should also be noted that neither probe can detect zero field intensity levels.

In conclusion, compare the measurements from your probes with probes of known accuracy--they are not replacements for certified laboratory grade models. At 950 KHz, with generally good results, these probes have been tested in H levels up to 1.55 A/m and E levels up to 742 V/m. Always follow good engineering and safety practices when constructing, and using, these devices. These probes are another valuable tool to help assure FCC OET-65B compliance.

Illustrations





Works Cited

"Units, Constants, and Conversion Factors." Reference Data For Radio Engineers. 5th ed. Indianapolis: Howard W. Sams & Co., 1973.

Back to Top  |  Back to Main Page

Site creation and design CopyrightŠ 1998 by Harry Sparks, KN4S